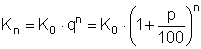am · an = am+n
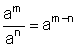
(am)n = am·n
(a · b)n = an · bn
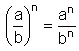
a0 = 1
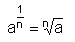
Potenzen
|
am · an = am+n |
(a · b)n = an · bn |
a0 = 1 |
Wurzeln
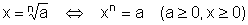
|
Logarithmen
y = loga(x) ⇔ x = ay (a > 0, a ≠ 1, b > 0)
loga(u · v) = loga(u) + loga(v) |
loga(1) = 0 |
Euler'sche Zahl (Basis des natürlichen Logarithmus ln): 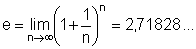
Exponentielles Wachstum: N(t) = N0·qt bzw. N(t) = N0·eλ·t, wobei λ = ln(q)
Zinseszinsen: