Normalform:
a · x + b · y = c
Lineare Funktion:
y = k · x + d
Parameterform:
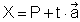
Normalvektorform:
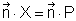
Punkt-Steigungs-Form:
y - y1 = k · (x - x1)
P: Punkt auf der Geraden, 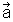 :
Richtungsvektor,
:
Richtungsvektor, 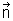 : Normalvektor
: Normalvektor
Geraden
Normalform: |
a · x + b · y = c |
Lineare Funktion: |
y = k · x + d |
Parameterform: |
|
Normalvektorform: |
|
Punkt-Steigungs-Form: |
y - y1 = k · (x - x1) |
P: Punkt auf der Geraden, |
|
Steigung der Geraden durch die Punkte P1 = (x1/y1) und P2 = (x2/y2): |
|
Anstiegswinkel: |
k = tan α |
Mittelpunkt einer Strecke: |
MAB = ½ · (A + B) |
Schwerpunkt eines Dreiecks: |
S = ⅓ · (A + B + C) |
Flächeninhalt eines Dreiecks |
|
Kreis
Hauptlage: M = (0/0) |
Allgemeine Lage: M = (xM/yM) |
x2 + y2 = r2 |
(x - xM)2 + (y - yM)2 = r2 |
Tangente in T = (xT/yT): |
|
xT · x + yT · y = r2 |
(xT - xM) · (x - xM) + (yT - yM) · (y - yM) = r2 |
Kegelschnitte
Ellipse |
Hyperbel |
Parabel |
Gleichung in 1. Hauptlage: |
||
|
|
y2 = 2px |
e2 = a2 - b2 |
e2 = a2 + b2 |
p = 2e |
Tangente in T = (xT/yT): |
||
|
|
yTy = p · (x + xT) |
2a: Hauptachse, 2b: Nebenachse, e: Brennweite (lineare Exzentrizität), p: Parameter |
||