Funktion:
Stammfunktion:
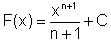
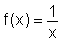
Funktion: |
Stammfunktion: |
| f(x) = k | F(x) = k · x + C |
| f(x) = xn (n ≠ -1) | 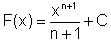 |
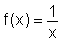 |
F(x) = ln |x| + C |
| f(x) = ex | F(x) = ex + C |
| f(x) = sin x | F(x) = -cos x + C |
| f(x) = cos x | F(x) = sin x + C |
Integrationsregeln
∫(f(x) ± g(x))dx = ∫f(x)dx ± ∫g(x)dx |
| ∫k·f(x)dx = k · ∫f(x) dx |
∫f(x)·g(x)dx = F(x)·g(x) - ∫F(x)·g'(x) dx |
∫f(g(x))·g'(x)dx = F(g(x)) |
Hauptsatz der Integralrechnung:
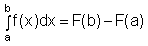 |
Flächen- und Volumsberechnungen
| Fläche zwischen Kurve und x-Achse: | 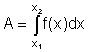 |
(x1, x2: Nullstellen) |
| Fläche zwischen zwei Kurven: | 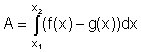 |
(x1, x2: Schnittpunkte) |
| Rotation um x-Achse: | 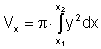 |
|
| Rotation um y-Achse: | 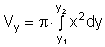 |