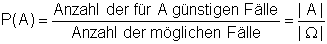
Ω: Ereignisraum (alle möglichen Ereignisse)
A, B ⊆ Ω: Ereignisse
A' = Ω \ A: Gegenereignis von AP(A): Wahrscheinlichkeit von A
P(B|A): Wahrscheinlichkeit von B unter der Bedingung A (bedingte Wahrscheinlichkeit)
|
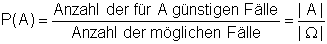Klassische Definition der Wahrscheinlichkeit |
| P(Ω) = 1 | sicheres Ereignis |
| P({ }) = 0 | unmögliches Ereignis |
| P(A') = 1 − P(A) | Wahrscheinlichkeit des Gegenereignisses |
| P(A ∪ B) = P(A) + P(B) | wenn A und B einander ausschließen |
| P(A ∪ B) = P(A) + P(B) - P(A ∩ B) | allgemein |
| P(A ∩ B) = P(A) · P(B) | wenn A und B voneinander unabhängig sind |
| P(A ∩ B) = P(A) · P(B|A) = P(B) · P(A|B) | allgemein |
| Anzahl der Anordnungen von n Elementen: |
|
|
| Anzahl der k-elementigen Teilmengen von n Elementen: |
|
Wahrscheinlichkeitsverteilungen
| Erwartungswert: |  |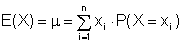
| Varianz: |  |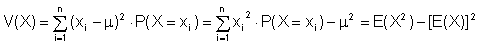
| Standardabweichung: |  |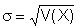
Binomialverteilung
n: Anzahl der Versuche
p: Wahrscheinlichkeit für einen Erfolg
q = 1 - p: Wahrscheinlichkeit für einen Misserfolg
X: Anzahl der Erfolge bei n Versuchen
 |
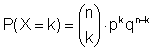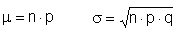
Hypergeometrische Verteilung
n: Anzahl der Versuche
N: Umfang der Grundgesamtheit
M: Anzahl der "guten" Elemente in der Grundgesamtheit
X: Anzahl der "guten" Elemente in einer Stichprobe von n Elementen
 |
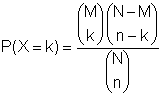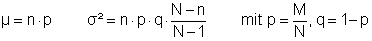
Normalverteilung
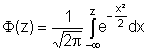Verteilungsfunktion der Standardnormalverteilung
P(Z ≤ z) = Φ(z) |
Φ(−z) = 1 − Φ(z) |
P(Z ≥ z) = 1 − Φ(z) |
P(z1 ≤ Z ≤ z2) = Φ(z2) − Φ(z1) |
P(−z ≤ Z ≤ z) = Φ(z) − Φ(-z) = 2 · Φ(z) − 1 |
Eine beliebige, normalverteilte Zufallsvariable wird durch die Standardisierungsformel
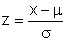
zu einer standardnormalverteilten Zufallsvariablen.
