Quadratische Gleichungen

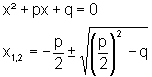
Eine Gleichung der Form

a · x² + b · x + c = 0

mit a, b, c ∈ R, a ≠ 0
heißt quadratische Gleichung.
Wir betrachten zunächst die normierte quadratische Gleichung:

x ² + p · x + q = 0

Sonderfälle:

• p = 0:

  x² − 4 = 0 | + 4
  x² = 4

  x_1,2 = ±2

  Achtung! Eine solche Gleichung hat zwei Lösungen: L = {−2, 2}

  x² + 1 = 0 | − 1
  x² = −1

  Hier gibt es keine reelle Lösung: L = { }

• q = 0:

  x² − 3 · x = 0
  x · (x − 3) = 0

  Ein Produkt ist genau dann 0, wenn ein Faktor 0 ist:

  x = 0 oder x − 3 = 0

  x₁ = 0, x_{2 = 3}

  Auch hier gibt es also zwei Lösungen: L = {0, 3}

Allgemeiner Fall:

Diesen Fall können wir durch Ergänzen auf ein vollständiges Quadrat lösen.
Beispiele:

• x² − 6 · x + 5 = 0 | − 5
  x² − 6 · x = −5 | + 9
  x² − 6 · x + 9 = 4
  (x − 3)² = 4
  x − 3 = ±2 | + 3

  x₁ = 1, x₂ = 5

• x² + 10 · x + 25 = 0
  (x + 5)^{2 = 0}
  x + 5 = 0

  x_1,2 = −5

• x² + 4 · x + 7 = 0 | − 7
  x² + 4 · x = −7 | + 4
  x² + 4 · x + 4 = −3
  (x + 2)² = −3

  keine Lösung

Eine quadratische Gleichung kann also zwei, eine oder gar keine Lösung haben. Im zweiten Fall spricht man auch von einer Doppellösung.

Führen wir diese Berechnung allgemein durch, so erhalten wir die kleine Lösungsformel für quadratische Gleichungen (wichtig!):

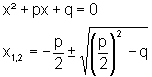
Den Ausdruck 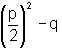bezeichnet man als Diskriminante D (von discriminare, unterscheiden).
Eine quadratische Gleichung hat

• zwei Lösungen, wenn D > 0
• eine Lösung, wenn D = 0
• keine Lösung, wenn D < 0

Die allgemeine Form der quadratischen Gleichung löst man mit der großen Lösungsformel:

Der Satz von Vieta

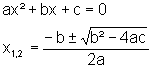
Wenn wir die Lösungen einer quadratischen Gleichung kennen, können wir die Gleichung rekonstruieren.
Beispiel: x₁ = 2, x₂ = 3
Diese Zahlen erfüllen sicher die Gleichung

(x − 2) · (x − 3) = 0

Durch Ausmultiplizieren erhalten wir die Normalform:

x ² − 5 · x + 6 = 0

Wir sehen also, dass p = −5 = −(2 + 3) und q = 6 = 2 · 3.
Allgemein:

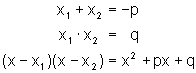
Die Bedeutung dieses Satzes besteht vor allem darin, dass man mit seiner Hilfe ein quadratisches Polynom in Linearfaktoren zerlegen kann, wenn die entsprechende Gleichung zwei reelle Lösungen (oder eine Doppellösung) hat.

Übungen

Links:

mathe online, Gleichungen, Abschnitt "Quadratische Gleichungen":
http://www.mathe-online.at/mathint/gleich/i.html#QuGl

Applets: Quadratische Gleichungen 1 (Beweis der kleinen Lösungsformel),
Quadratische Gleichungen 2 (Gegenüberstellung verschiedener Lösungsmethoden)

Weiter: Gleichungen 3. und höheren Grades