Gleichungen mit mehreren Unbekannten

Produktmenge

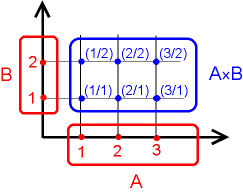
Die Produktmenge A × B (sprich "A kreuz B") zweier Mengen A und B besteht aus allen geordneten (Zahlen-)Paaren, deren erstes Element in A und deren zweites Element in B enthalten ist.

A × B = {(x/y) / (x ∈ A) und (y ∈ B)}

Bsp.: A = {1, 2, 3}, B = {1, 2}
A × B = {(1/1), (1/2), (2/1), (2/2), (3/1), (3/2)}

Graphische Veranschaulichung:

Für ℝ × ℝ schreibt man auch ℝ². Die Elemente dieser Menge entsprechen allen Punkten der Ebene.

Analog definiert man A × B × C als Menge von geordneten (Zahlen-)Tripeln.
ℝ × ℝ × ℝ = ℝ³ entspricht dabei allen Punkten des Raumes.

Näheres zum rechtwinkligen Koordinatensystem - Übungen dazu

Eine lineare Gleichung mit zwei Unbekannten

Allgemeine Form:

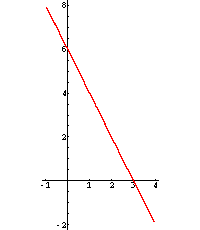
a·x + b·y = c

(a, b, c ∈ R, a und b nicht beide 0)

Es gibt unendlich viele Zahlenpaare (Elemente von ℝ²), die diese Gleichung lösen, z.B.
L = {(0/6), (1/4), (2/2), (3/0) ...}

Zeichnen wir die entsprechenden Punkte in ein Koordinatensystem ein, so sehen wir, dass sie auf einer Geraden liegen:

Lineare Gleichungssysteme mit zwei Unbekannten

Beispiel:

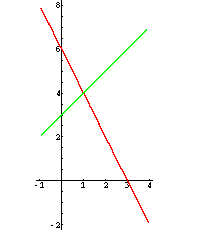
I:	2·x + y	= 6
II:	x − y	= −3

Wir suchen ein Zahlenpaar, das beide Gleichungen löst. Das entspricht dem Schnittpunkt der zugehörigen Geraden.

Der Schnittpunkt hat die Koordinaten S(1/4), die Lösung des Gleichungssystems lautet daher: x = 1, y = 4 bzw. L = {(1/4)}..

Zur rechnerischen Lösung gibt es verschiedene Methoden:

Einsetzungsmethode:

Eine Unbekannte wird aus einer Gleichung ausgedrückt und in die zweite Gleichung eingesetzt:

I:	y	= 6 − 2·x
in II:	x − (6 − 2·x)	= −3
	3·x − 6	= −3
	x	= 1

Durch Einsetzen von x in die umgeformte erste Gleichung erhält man y.

Gleichsetzungsmethode:

Aus beiden Gleichungen wird dieselbe Unbekannte ausgedrückt; die beiden Ausdrücke werden gleichgesetzt.

I:	y	= 6 − 2·x
II:	y	= x + 3
	6 − 2·x	= x + 3
	x	= 1

Eliminationsmethode:

Die beiden Gleichungen werden addiert. Vorher multipliziert man sie, wenn nötig, mit geeigneten Konstanten, so dass beim Addieren eine Unbekannte wegfällt.

I:	2·x + y	= 6
II:	x − y	= −3
	3·x	= 3
	x	= 1

Noch ein Beispiel:

I:	2·x + 5·y	= 11	| ·3
II:	3·x + 4·y	= 6	| ·(−2)
I:	6·x + 15·y	= 33
II:	−6·x − 8·y	= −12
	7·y	= 21
	y	= 3

Das Ergebnis setzt man in irgendeine der beiden Gleichungen ein, um die zweite Unbekannte zu erhalten.

Sonderfälle

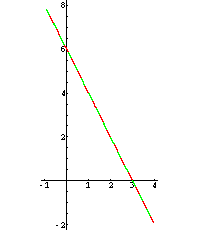
I:	2·x + y	= 6
II:	4·x + 2·y	= 12

Die eine Gleichung ist ein Vielfaches (hier: das Doppelte) der anderen.

Beide Gleichungen entsprechen derselben Geraden; es gibt unendlich viele Lösungen.

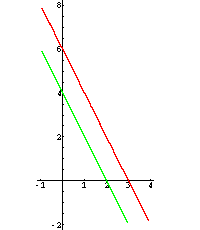
I:	2·x + y	= 6
II:	4·x + 2·y	= 8

Die linke Seite der einen Gleichung ist ein Vielfaches (hier: das Doppelte) der anderen, die rechte nicht.

Die entsprechenden Geraden sind parallel; es gibt keine Lösung: L = { }

Lineare Gleichungssysteme mit drei Unbekannten

Die Lösungsmenge einer Gleichung der Form

a·x + b·y + c·z = d

besteht aus unendlich vielen Zahlentripeln. Die entsprechenden Punkte liegen auf einer Ebene im ℝ³.

Die Lösung eines Systems von drei Gleichungen mit drei Unbekannten entspricht daher dem Schnitt dreier Ebenen. Die Lösungsmenge kann aus einem Punkt, einer Geraden oder einer Ebene bestehen oder ganz leer sein.

Einige Lösungsfälle:

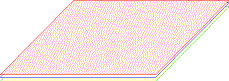
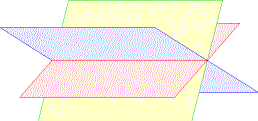
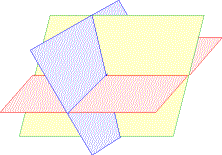
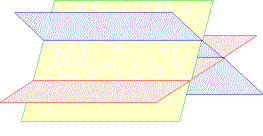
Beispiel für Eliminationsmethode:

I:	x   + y   − z	= 6
II:	−x + 2·y + 3·z	= 7
III:	2·x − 3·y + 2·z	= 5
3·I:	3·x + 3·y − 3·z	= 18
II:	−x + 2·y + 3·z	= 7
IV:	2·x + 5·y	= 25
2·I:	2·x + 2·y − 2·z	= 12
III:	2·x − 3·y + 2·z	= 5
V:	4·x − y	= 17
IV:	2·x + 5·y	= 25
5·V:	20·x − 5·y	= 85
	22·x	= 110
	x	= 5
in V:	4·5 − y	= 17
	y	= 3
in I:	5 + 3 − z	= 6
	z	= 2

(Wichtig dabei ist, dass man in den ersten beiden Schritten beide Male dieselbe Variable eliminiert!)

Übungen - Textaufgaben