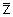 = a − b·i
= a − b·iBekanntlich haben quadratische Gleichungen nicht immer eine reelle Lösung. Wenn man will, dass quadratische Gleichungen (und solche höheren Grades) ohne Einschränkungen lösbar sein sollen, muss man eine neue Art von Zahlen einführen.
Wir definieren die imaginäre Einheit i durch die Gleichung
i2 = −1
(Das ist keine reelle Zahl, weil das Quadrat einer rellen Zahl immer positiv oder 0 ist.)
Vielfache von i heißen imaginäre Zahlen (z.B. 2·i, −0,5·i, √3·i).
Eine Zahl der Form
Die Menge aller komplexen Zahlen bezeichnet man mit ℂ.
Die Menge ℝ ist eine Teilmenge von ℂ; sie besteht aus allen Zahlen, deren Imaginärteil 0 ist.
Beispiel: Die Gleichungx2 − 2·x + 10 = 0 hat die Lösungen
x1,2 = 1 ± √−9 = 1 ± 3·√−1, also
x1 = 1 + 3·i, x2 = 1 − 3·i
Zwei solche Zahlen, die sich nur durch das Vorzeichen des Imaginärteils unterscheiden,
heißen konjugiert komplex, mit anderen Worten: die zu 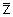 = a − b·i
= a − b·i
Bei Addition, Subtraktion und Multiplikation gelten dieselben Rechenregeln wie beim Rechnen mit Termen. Wenn in der Rechnung i2 auftritt, wird es durch −1 ersetzt.
Beispiel:
(2 + i) + (1 + 3·i) = 2 + i + 1 + 3·i = 3 + 4·i
(2 + i) − (1 + 3·i) = 2 + i − 1 − 3·i = 1 − 2·i
(2 + i)·(1 + 3·i) = 2 + i + 6·i + 3·i2 = −1 + 7·i
Wenn man durch eine komplexe Zahl dividiert, erweitert man mit der konjugiert komplexen Zahl.
Es ist nämlich
Beispiel:
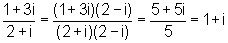
Man kann komplexe Zahlen auch in einem rechtwinkeligen Koordinatensystem darstellen.
Die erste Achse ist die reelle, die zweite die imaginäre Achse.
Die Zahl
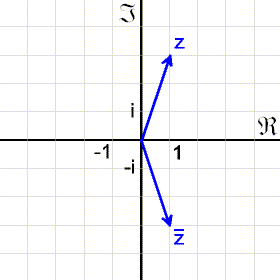
Konjugiert komplexe Zahlen liegen symmetrisch zur reellen Achse.
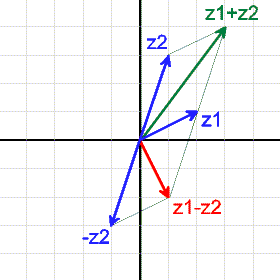
Addition und Subtraktion entsprechen der üblichen Vektoraddition und -subtraktion.
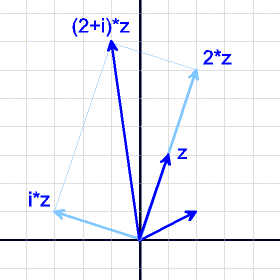
Eine Multiplikation mit einer reellen Zahl ist eine Streckung, Multiplikation mit i ergibt eine Drehung um 90°.
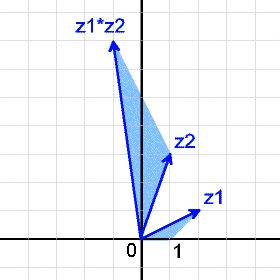
Die Dreiecke O1Z1 und OZ2(Z1·Z2) sind zueinander ähnlich.
Man kann eine komplexe Zahl auch durch ihren Betrag |z| (Abstand vom Nullpunkt) und ihr Argument φ (Winkel, den sie mit der x-Achse einschließt) angeben:
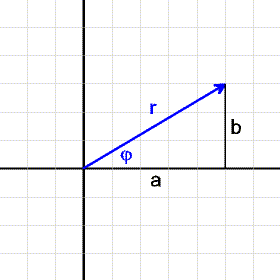
|
|
a = r·cos(φ) b = r·sin(φ) |
Wir können daher auch schreiben:
(Man vereinbart meist, dass φ zwischen 0° und 360° liegen soll. Weil die Umkehrung der Tangensfunktion nicht eindeutig ist, sollte man bei der Berechnung von φ immer eine Skizze machen!)
Die Multiplikation und Division von komplexen Zahlen ist in der Polardarstellung
ziemlich einfach. Die Multiplikation mit
(r1; φ1)·(r2; φ2) = (r1·r2; φ1 + φ2)
(r; φ)n = (rn; n·φ)
Die letzte Gleichung schreibt man oft in anderer Form (Formel von de Moivre):
[r·(cos(φ) + i·sin(φ))]n = rn·(cos(n·φ) + i·sin(n·φ))
Die Regeln für das Wurzelziehen sind analog, aber Achtung:
Wenn man zum Argument einer komplexen Zahl ein Vielfaches von 360° addiert, ändert sich die Zahl nicht.
Wenn man zum Argument von z ein Vielfaches von 360°/n addiert, ändert sich zn nicht.
Fürn√z gibt es daher n verschiedene Möglichkeiten:
(k = 0, 1, ..., n−1)
Im Reellen gilt:
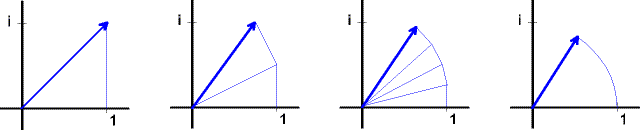
Die ersten drei Bilder zeigen
ei·φ = cos(φ) + i·sin(φ) (φ im Bogenmaß)
Die Polardarstellung einer komplexen Zahl wird daher zu
Setzt man φ = π (= 180°), so erhält man die bemerkenswerte Gleichung
ei·π = −1
Ausführliche Erklärungen:
Lernpfad "Komplexe Zahlen" von Andreas Pester: http://www.mathe-online.at/lernpfade/complex/
Dave's Short Course on Complex Numbers (englisch): http://www.clarku.edu/~djoyce/complex/
Lernziele:
Geschichte der komplexen Zahlen
Eine Anwendung der komplexen Zahlen: Komplexe Wechselstromrechnung