Logarithmen

Im Kapitel "Potenzen und Wurzeln" haben wir den Ausdruck a^x für alle rationalen x erklärt. Für reelle (irrationale) Zahlen x kann man a^x mit beliebiger Genauigkeit annähern.

Man kann daher den Vorgang des Potenzierens auch umkehren und z.B. fragen: 2 hoch welche Zahl ergibt 5? Die gesuchte Hochzahl nennt man Logarithmus von 5 zur Basis 2.

Beispiel: log₂(8) = 3, weil 2³ = 8
(Die Klammer kann auch weggelassen werden.)

Spezielle Logarithmen:

Dekadischer Logarithmus (Basis 10):	log10 = lg (Taschenrechner: log)
Natürlicher Logarithmus (Basis e = 2,71828...):	loge = ln
Binärer Logarithmus (Basis 2):	log2 = ld (oder lb)

Rechengesetze

Da Logarithmen Hochzahlen sind, ergeben sich die Rechengesetze aus den Rechengesetzen für Potenzen:

Außerdem folgt aus der Definition des Logarithmus:

Beispiele:

• log = 3·log(a) + log(b) − 2·log(c)
• log (√5) = ¹/₂ · log(5)

(Die Basis des Logarithmus muss nicht angegeben werden, da die Rechenregeln für jede beliebige Basis gelten.)

Vor der Erfindung des Taschenrechners führte man komplizierte Berechnungen mithilfe von Logarithmentabellen durch (oder dem Rechenschieber, der auch auf Logarithmen beruht). Heute brauchen wir vor allem die 3. Rechenregel, um Exponentialgleichungen zu lösen (d.h. Gleichungen, bei denen die Unbekannte im Exponenten steht).

Exponentialgleichungen

Mit Hilfe des Logarithmus können wir jetzt die Frage von oben beantworten: 2 hoch wieviel ergibt 5?

2^x = 5
beide Seiten logarithmieren:
x · log(2) = log(5)
≈ 2,322

Ein etwas schwierigeres Beispiel:

2^3x−1 = 10^x
(3x − 1)·log(2) = x·log(10)
x·(3·log(2) − log(10)) = log(2)
≈ −3,106

Im Allgemeinen ist es egal, ob man dabei dekadische oder natürliche Logarithmen verwendet. Wenn in der Gleichung die Euler'sche Zahl e als Basis vorkommt, sollte man mit natürlichen Logarithmen rechnen. Dadurch vereinfacht sich die Rechnung, weil ln(e) = 1.

e^0,1x = 25
0,1x (·ln(e)) = ln(25)
x = ≈ 32,189

(Auf modernen Taschenrechnern kann man mit dem "solve"-Befehl auch Exponentialgleichungen lösen.)

Logarithmische Skalen

Auf einer logarithmischen Skala entsprechen gleiche Abstände (im Unterschied zu einer linearen Skala) immer der Multiplikation mit der gleichen Zahl (meist 10). Dadurch kann man große Wertebereiche übersichtlich darstellen, wie zum Beispiel hier die Massen verschiedener Tiere:

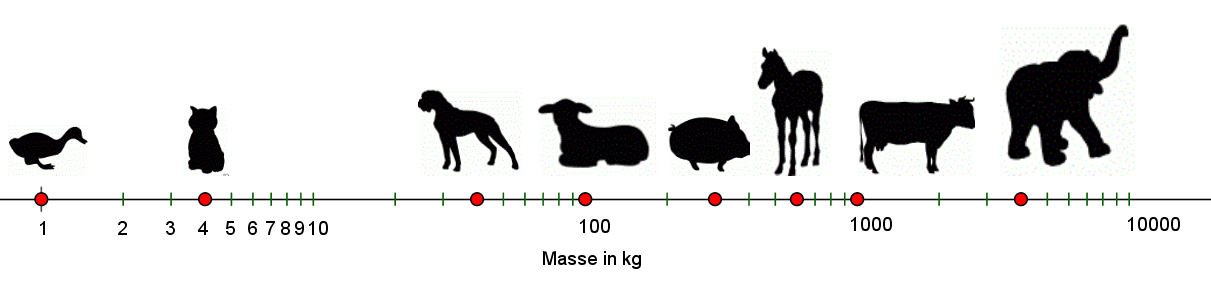
Auf einer linearen Skala würden sich die meisten Punkte am Anfang drängen, der Großteil der Achse wäre leer.
(Siehe auch die Darstellung des elektromagnetischen Spektrums auf Wikipedia.)

In den Naturwissenschaften verwendet man oft logarithmische Skalen, zum Beispiel:

• Richterskala für die Stärke von Erdbeben
• Dezibelskala in Akustik (Schalldruckpegel) und Elektrotechnik (Spannungspegel)
• pH-Wert für die Stärke einer Säure oder Lauge

und vieles mehr.

Übungen