Die Definitionen aus dem vorigen Abschnitt sind nur sinnvoll für Winkel zwischen 0° und 90°. Die folgende Definition gilt für beliebige Winkel:
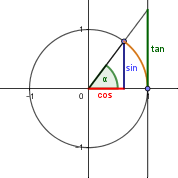
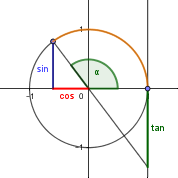
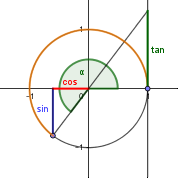
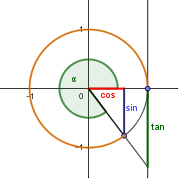
Wir zeichnen einen Kreis um den Koordinatenursprung mit dem Radius 1 und eine Gerade durch den Koordinatenursprung, die mit der positiven x-Achse den Winkel α einschließt. Der Schnittpunkt dieser Geraden mit dem Einheitskreis hat dann die Koordinaten (cos α / sin α), der Schnittpunkt mit der Tangente in (1/0) hat die Koordinaten (1 / tan α). Man kann also die Werte der Winkelfunktionen wie auf den Abbildungen ablesen (blau: sin α, rot: cos α, grün: tan α). Dabei muss auch auf das Vorzeichen geachtet werden.




(Überlege dir, dass diese Definitionen für 0° < α < 90° mit denen aus dem vorigen Abschnitt übereinstimmen!)
Die Umkehrung ist allerdings nicht mehr eindeutig - zu einem zulässigen Wert des Sinus (Cosinus, Tangens) gibt es zwei Winkel zwischen 0° und 360°. Es gilt:
sin(α) = sin(180° − α)
cos(α) = cos(360° − α)
tan(α) = tan(180° + α)
Ein "natürliches" Maß für die Größe eines Winkels ist die Länge des dazugehörigen Kreisbogens im Einheitskreis (in den Abbildungen oben orange). Die Einheit Radiant (rad) wird meistens weggelassen. Der Umfang des ganzen Kreises beträgt 2πm, daher sind 360° im Bogenmaß 2π rad. 1 rad entspricht 180°/π ≈ 57,3°.
| α in Grad | α in rad |
| 360° | 2π |
| 180° | π |
| 1° | π/180 |
Nun können wir die Graphen der Winkelfunktionen zeichnen (blau: Sinus, rot: Cosinus, grün: Tangens). Als x-Werte verwenden wir dabei das Bogenmaß der Winkel.
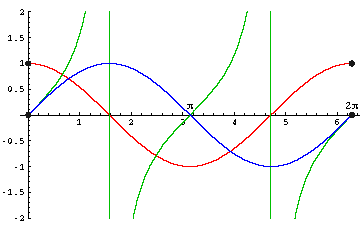
Für Winkel unter 0 oder über 2π (= 360°) wiederholen sich die Funktionswerte immer wieder. Man bezeichnet solche Funktionen als periodische Funktionen.
GeoGebra-Animationen:
Winkelfunktionen im Einheitskreis (ziehe den blauen Punkt auf dem Kreis)
Sinus Umkehrung (wähle einen Sinuswert, indem du den Punkt auf der y-Achse verschiebst)
Cosinus Umkehrung (verschiebe den roten Punkt auf der x-Achse)
Tangens Umkehrung (verschiebe den grünen Punkt auf der Tangente)
Lernziele