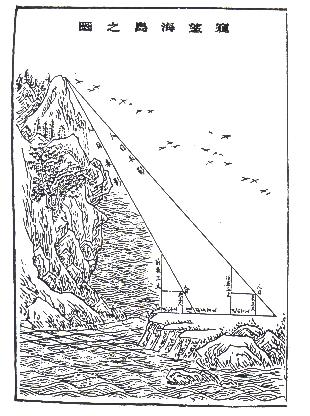
Die folgende Aufgabe stammt aus der "Mathematischen Inselsammlung" des chinesischen Mathematikers Liu Hui (263 n.Chr.):

Beobachte eine Insel, deren Höhe und Entfernung unbekannt ist. Errichte zwei Messlatten der Höhe 5 bu (chinesische Maßeinheit, 1 bu ≈ 1,67 m); die Entfernung zwischen beiden ist 1000 bu. Die beiden Stangen und die Insel sollen in einer Linie liegen. Gehe 123 bu von der ersten Stange zurück und beobachte den Berggipfel vom Boden aus; man sieht, dass das Ende der Stange mit dem Gipfel zusammenfällt. Dann gehe 127 bu von der zweiten Stange zurück und beobachte wieder den Gipfel vom Boden aus; die Spitze der Stange fällt mit dem Gipfel zusammen. Wie hoch ist die Insel, und wie weit ist sie von der vorderen Stange entfernt?
Löse die Aufgabe mithilfe der Trigonometrie (berechne zuerst die Höhenwinkel). Dann vergleiche dein Ergebnis mit Liu Huis Lösung (markiere den Text, um ihn anzuzeigen):
(Antwort:) Die Höhe der Insel ist 4 li 55 bu. Sie ist 102 li 150 bu von der Stange entfernt.
(Methode:) Multipliziere den Abstand der Stangen mit der Höhe der Stangen, das ergibt den Zähler. Nimm die Differenz der Abstände der Beobachtungspunkte (von den Stangen) als Nenner, durch den der Zähler zu dividieren ist. Dazu addiere die Höhe der Stangen; das Ergebnis ist die Höhe der Insel. - Um die Entfernung der Insel zu finden, multipliziere die Strecke, um die man von der ersten Stange zurückgegangen ist, mit dem Abstand zwischen den Stangen; das ergibt den Zähler. Nimm die Differenz der Abstände der Beobachtungspunkte (von den Stangen) als Nenner, durch den der Zähler zu dividieren ist. Das Ergebnis ist die Entfernung der Insel von der vorderen Stange.
(1 li = 300 bu)