Zahlenmengen

Menge der natürlichen Zahlen

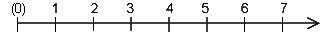
ℕ = {0, 1, 2, 3, 4, 5, ... }

Die natürlichen Zahlen benutzen wir im Alltag, um Gegenstände zu zählen. Es gibt unendlich viele natürliche Zahlen. (Die 0 wird nicht immer dazugerechnet.)

Veranschaulichung auf dem Zahlenstrahl:

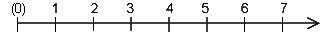
Man kann die natürlichen Zahlen auf verschiedene Art einteilen, z.B.
gerade Zahlen (ℕ_g) und ungerade Zahlen (ℕ_u)
Primzahlen (ℙ) und zusammengesetzte Zahlen
(Jede natürliche Zahl kann eindeutig als Produkt von Primzahlen geschrieben werden, z.B. 60 = 2·2·3·5)

Wenn wir zwei natürliche Zahlen addieren oder multiplizieren, ist das Ergebnis wieder eine natürliche Zahl. Subtraktion ist nicht immer möglich (z.B. 7 - 10 = ?). Daher erweitern wir die natürlichen Zahlen zur

Menge der ganzen Zahlen

ℤ = { ... -3, -2, -1, 0, 1, 2, 3, ... }

Veranschaulichung auf der Zahlengeraden:

Rechnen mit negativen Zahlen

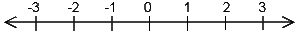
Innerhalb der ganzen Zahlen ist die Addition, Subtraktion und Multiplikation uneingeschränkt möglich, die Division nicht unbedingt (z.B. 2 : 3 = ?). Wir nehmen daher auch die Brüche (Quotienten zweier ganzer Zahlen) dazu und erhalten so die

Menge der rationalen Zahlen

(Menge aller Brüche von der Form p/q, wobei p und q ganze Zahlen sind und q nicht 0 ist.)

(Die Bezeichnung "rational" kommt von lat. ratio: Verhältnis, weil man einen Bruch auch als Verhältnis zwischen zwei ganzen Zahlen auffassen kann. Die ganzen Zahlen sind rationale Zahlen mit dem Nenner 1.)

Die rationalen Zahlen liegen auf der Zahlengeraden zwischen den ganzen Zahlen:

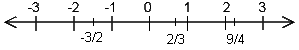
Jede rationale Zahl kann als abbrechende oder periodische Dezimalzahl geschrieben werden.

Rechnen mit Brüchen

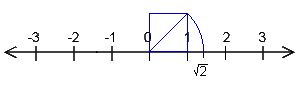
Zwischen zwei Zahlen haben immer noch unendlich viele weitere rationalen Zahlen Platz - man sagt, die rationalen Zahlen liegen "dicht" auf der Zahlengeraden. Trotzdem gibt es dazwischen noch unendlich viele irrationale Zahlen (nicht abbrechende, nicht periodische Dezimalzahlen)!

(Beweis, dass √2 keine rationale Zahl ist)

Die rationalen und irrationalen Zahlen bilden zusammen die

Menge der reellen Zahlen

Die Menge ℝ besteht aus allen Punkten der Zahlengeraden.

In ℝ können wir jetzt uneingeschränkt addieren, subtrahieren, multiplizieren, dividieren (außer durch 0) und Wurzeln ziehen, mit einer Ausnahme:
Weil das Quadrat einer reellen Zahl immer positiv ist, hat eine Gleichung wie z.B. x² = -1 keine reelle Lösung. Wenn wir solche Gleichunge auch lösen wollen, müssen wir den Zahlenbereich ein letztes Mal erweitern zur

Menge der komplexen Zahlen

Wir definieren die imaginäre Einheit i durch i² = -1.

ℂ = {a + b · i | a, b ∈ ℝ}
(Menge aller Zahlen von der Form a + bi, wobei a und b reelle Zahlen sind)

i kann nicht auf der Zahlengeraden liegen, aber man kann sich die komplexen Zahlen mithilfe der Gauss'schen Zahlenebene veranschaulichen:

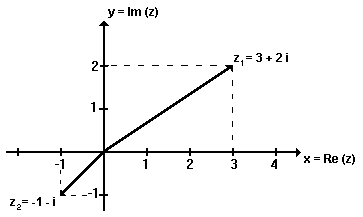
(Die x-Achse wird als reelle Achse, die y-Achse als imaginäre Achse bezeichnet.)

Eine etwas ausführlichere Erklärung gibt es auf mathe online:
http://www.mathe-online.at/mathint/zahlen/i.html, Abschnitt "Zahlenmengen"