Der Binomische Lehrsatz lautet:
Dieses Zahlendreieck war schon im Mittelalter indischen, persischen und chinesischen Mathematikern bekannt. Mit seiner Hilfe kann man die Potenzen von Binomen berechnen. Seinen Namen hat es von Blaise Pascal (1623 - 1662), der es im Zusammenhang mit der Wahrscheinlichkeitsrechnung untersuchte.
Bildungsvorschrift: Die erste und letzte Zahl jeder Reihe ist 1; die übrigen Zahlen erhält man, indem man jeweils die beiden darüberstehenden Zahlen addiert.
1 1
1 2 1
1 3 3 1
1 4 6 4 1
1 5 10 10 5 1
1 6 15 20 15 6 1
1 7 21 35 35 21 7
1
1 8 28 56 70 56 28
8 1
1 9 36 84 126 126 84 36
9 1
1 10 45 120 210 252 210 120 45 10
1
1 11 55 165 330 462 462 330 165 55
11 1
1 12 66 220 495 792 924 792 495 220
66 12 1
und so weiter...
Diese Zahlen treten, wie erwähnt, auf, wenn man die Potenzen eines Binoms berechnet - deshalb heißen sie Binomialkoeffizienten.
Die k-te Zahl in der n-ten Reihe (wobei man bei 0 zu zählen anfangen muss) bezeichnet man mit ![]() (sprich: "n über k"). Andere Bezeichnungen sind binom(n, k) oder nCr ("n choose r").
(sprich: "n über k"). Andere Bezeichnungen sind binom(n, k) oder nCr ("n choose r").
Der Binomische Lehrsatz lautet:
Z.B.:
(meist werden die Potenzen in umgekehrter Reihenfolge angeschrieben).
Sie begegnen uns aber auch in der Wahrscheinlichkeitsrechnung: Wenn ein Ereignis mit der Wahrscheinlichkeit p eintritt, so beträgt die Wahrscheinlichkeit, dass es bei n Versuchen k-mal eintritt,
Z.B. ist die Wahrscheinlichkeit, dass man bei 4-maligem Würfeln genau 2 Sechser wirft, 6·(1/6)2·(5/6)2 = 0,1157. Das ist die sogenannte Binomialverteilung.
Wir schreiben die Potenz einmal ausführlich auf:
Bei der Multiplikation wird aus jeder Klammer entweder a oder b ausgewählt. a3b2 entsteht zum Beispiel, wenn wir 3 a's und 2 b's wählen, etwa aabab. Wie viele Möglichkeiten gibt es dafür?
Wenn wir 5 verschiedene Elemente anordnen wollen, z.B. abcde, gibt es für den ersten Platz 5 Möglichkeiten, für den zweiten nur mehr 4, für den dritten 3, ...
also insgesamt
Es gibt n! Möglichkeiten, n verschiedene Elemente anzuordnen.
Die 3 a's können aber auf
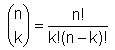
Es gibt ![]() Möglichkeiten, n Elemente anzuordnen, von denen jeweils k und
Möglichkeiten, n Elemente anzuordnen, von denen jeweils k und
Oder:
Es gibt ![]() Möglichkeiten, aus einer Menge von n Elementen k auszuwählen,
wobei es nicht auf die Reihenfolge ankommt.
Möglichkeiten, aus einer Menge von n Elementen k auszuwählen,
wobei es nicht auf die Reihenfolge ankommt.
Am Pascal'schen Dreieck kann man eine Fülle von interessanten Beziehungen entdecken:
 In den Schrägreihen stehen die sogenannten
figurierten Zahlen:
In den Schrägreihen stehen die sogenannten
figurierten Zahlen:
in der ersten Reihe die natürlichen Zahlen (n),
in der zweiten die Dreieckszahlen (D(n) = 1 + 2 + ... + n),
in der dritten die Tetraederzahlen (T(n) = D(1) + D(2) + ... + D(n)) usw.
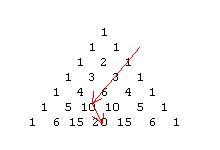 Addiert man die ersten Zahlen einer Schrägreihe, so erhält man die Zahl, die schräg
unter dem letzten Summanden steht.
Addiert man die ersten Zahlen einer Schrägreihe, so erhält man die Zahl, die schräg
unter dem letzten Summanden steht.
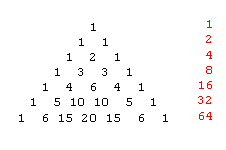 Die Summe der Zahlen in der n-ten Horizontalreihe beträgt 2n
Die Summe der Zahlen in der n-ten Horizontalreihe beträgt 2n
(das kann man leicht beweisen, indem man in der binomischen Formel
Wenn man die Zahlen abwechselnd addiert und subtrahiert, ist das Ergebnis 0 (außer in der nullten Reihe).
(Setze a = 1, b = −1)
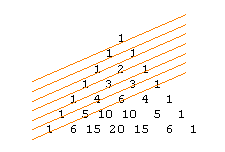 Und wenn man die Zahlen in den "Diagonalen" addiert, erhält man die Fibonacci-Zahlen.
Und wenn man die Zahlen in den "Diagonalen" addiert, erhält man die Fibonacci-Zahlen.