Definition: Ein Kreis ist die Menge aller Punkte der Ebene, die von einem Punkt M
denselben Abstand r haben.k = {X | XM = r}
Definition: Ein Kreis ist die Menge aller Punkte der Ebene, die von einem Punkt M
denselben Abstand r haben.
k = {X | XM = r}
Daraus erhalten wir die Gleichung:
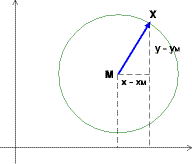
k: |X − M| = r ⇒ (X − M)2 = r2
In Koordinatenform ergibt das:
k: (x − xM)2 + (y − yM)2 = r2
wobei (xM/yM) die Koordinaten des Mittelpunktes sind.
Liegt der Mittelpunkt im Koordinatenursprung (Hauptlage), so lautet die Gleichung einfach:
k: x2 + y2 = r2
Beispiele:
Ein Kreis hat den Mittelpunkt M(2/1) und den Radius r = 5.
Die Gleichung des Kreises lautet:
k: (x − 2)2 + (y − 1)2 = 25
Das können wir noch umformen:
x2 − 4x + 4 + y2 − 2y + 1 = 25
x2 + y2 − 4x − 2y − 20 = 0
Ein Kreis hat den Mittelpunkt M(−3/2) und geht durch den Punkt P(1/4).
Der Radius ist der Abstand MP, d.h. der Betrag des Vektors MP:
r = √(42 + 22) = √20
k: (x + 3)2 + (y − 2)2 = 20
Die Gleichung eines Kreises lautet:
x2 + y2 − 10x + 6y + 18 = 0
Ermittle Mittelpunkt und Radius!
Wir ordnen die Gleichung um und ergänzen auf vollständige Quadrate:
x2 −10x + y2 + 6y = −18
x2 − 10x + 25 + y2 + 6y + 9 = −18 + 25 + 9
(x − 5)2 + (y + 3)2 = 16
⇒ M(5/-3), r = 4
Ob ein Punkt auf einem Kreis liegt, kann man feststellen, indem man seine Koordinaten in die Kreisgleichung einsetzt.
Wird ein Kreis mit einer Geraden oder zwei Kreise miteinander geschnitten,
so kann es zwei, eine oder gar keine Lösung geben.
Beispiele:
k: x2 + y2 = 25, g: y = 2x − 5
k ∩ g: x2 + (2x − 5)2 = 25 ⇒
x1 = 0, x2 = 4
in g einsetzen ⇒ y1 = −5, y2 = 3
Es gibt also zwei Schnittpunkte: S1(0/−5), S2(4/3)
k: x2 + y2 = 20, g: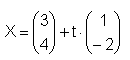 
x = 3 + t, y = 4 - 2t in die Kreisgleichung einsetzen:
(3 + t)2 + (4 − 2t)2 = 20 ⇒ t = 1
⇒ T(4/2)
Die Gerade berührt den Kreis im Punkt T, sie ist also eine Tangente.
k1: x2 + y2 − 4 = 0, k2: x2 + y2 − 12x + 32 = 0
Wir subtrahieren die Gleichungen voneinander und erhalten x = 3.
Wenn wir das in k1 einsetzen, kommen wir auf y2 = −5, es gibt also keine Lösung.
Die zwei Kreise schneiden einander nicht.
Im Raum erhalten wir ganz analog die Gleichung der Kugel:
k: (X − M)2 = r2
k: (x − xM)2 + (y − yM)2 + (z − zM)2 = r2
Die Tangente an einen Kreis steht immer normal auf den Radius im Berührpunkt. Wir können daher sofort die Gleichung der Tangente im Punkt T anschreiben, wobei MT der Normalvektor ist.
Beispiel:
k: (x − 1)2 + (y + 1)2 = 10 (d.h. der Mittelpunkt hat die Koordinaten M(1/−1))
Wie lautet die Gleichung der Tangente im Punkt T(2/2)?
t: x + 3y = 8
Der Schnittwinkel von Gerade und Kreis ist definiert als der Winkel, den die Gerade mit der Tangente im Schnittpunkt einschließt. Ebenso ist der Schnittwinkel zweier Kreise der Winkel zwischen den Tangenten im Schnittpunkt. (Dabei ist es egal, welchen Schnittpunkt man betrachtet - Symmetrie!)
Im Raum erhält man analog die Gleichung der Tangentialebene an eine Kugel.
Lernziele
