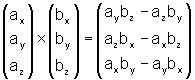Vektorrechnung im Raum

Das vektorielle Produkt

Im ℝ³ gibt es außer dem Skalarprodukt noch ein weiteres Vektorprodukt, das vektorielle Produkt a×b (sprich: "a kreuz b"). Es ist so definiert:

• a×b ist ein Vektor, der auf a und b normal steht.

• Der Betrag des vektoriellen Produkts ist gleich der Fläche des Parallelogramms, das von a und b aufgespannt wird:
  |a×b| = |a|·|b|·sin(α)

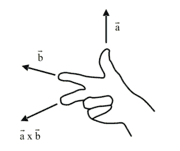
• Die Vektoren a, b und a×b bilden ein Rechtssystem, das heißt, sie sind so angeordnet wie Daumen, Zeigefinger und Mittelfinger der rechten Hand (Rechte-Hand-Regel).

Es gilt das Assoziativ- und das Distributivgesetz, aber nicht das Kommutativgesetz: b×a = −a×b (!)

Wir untersuchen die Produkte der Einheitsvektoren e_x, e_y und e_z:

e_x×e_x = 0, e_y×e_y = 0, e_z×e_z = 0
e_x×e_y = e_z, e_y×e_z = e_x, e_z×e_x = e_y
e_y×e_x = −e_z, e_z×e_y = −e_x, e_x×e_z = −e_y

Daraus leiten wir folgende Formel ab:

Grundaufgaben der Vektorrechnung im ℝ³

Zur Erinnerung: Geradengleichungen kann man im Raum nur in der Parameterform angeben. Für Ebenengleichungen verwendet man am besten die Normalform. Wenn zwei Richtungsvektoren der Ebene gegeben sind, ist ihr vektorielles Produkt ein Normalvektor.

Schnittpunkte und -geraden

• Zwei Geraden g: X = A + t·a, h: X = B + s·b
  Die Geraden können einander schneiden, parallel oder windschief sein.

  Wenn die Richtungsvektoren nicht parallel sind, setzt man die rechten Seiten der Geradengleichungen gleich. Man erhält drei Gleichungen mit zwei Unbekannten. Aus zwei Gleichungen kann man s und t berechnen. Wenn das auch eine Lösung der dritten Gleichung ist, schneiden die Geraden einander (den Schnittpunkt erhält man, indem man s oder t in die entsprechende Geradengleichung einsetzt). Sonst sind sie windschief.

  Wenn die Richtungsvektoren parallel sind, fallen die Geraden entweder zusammen oder sie sind parallel. Das erkennt man am besten am Vektor AB.

• Zwei Ebenen: Der Richtungsvektor der Schnittgeraden ist das vektorielle Produkt der beiden Normalvektoren. Einen Punkt kann man durch Probieren finden, z.B. indem man z = 0 setzt.

  Wenn die Normalvektoren parallel sind, fallen die Ebenen zusammen oder sind parallel, je nachdem ob die rechten Seiten der Ebenengleichungen übereinstimmen oder nicht.

• Gerade und Ebene: Man schreibt die Geradengleichung zeilenweise auf und setzt die Ausdrücke für x, y und z in die Ebenengleichung ein.

Abstände

• Zwei Punkte P, Q: der Abstand ist der Betrag des Vektors PQ.

• Punkt P und Gerade g: Man legt durch P eine Ebene, die auf g normal steht, und berechnet ihren Schnittpunkt S mit g. Der gesuchte Abstand ist der Betrag des Vektors PS.

  Oder: d(P,g) = |AP×a₀|       (A ist ein Punkt auf g, a₀ der Einheitsvektor zum Richtungsvektor a).

• Punkt P und Ebene ε: Man legt durch P eine Gerade, die auf ε normal steht, und berechnet ihren Schnittpunkt S mit ε. Auch hier ist der gesuchte Abstand der Betrag des Vektors PS.

  Oder: d(P,ε) = |AP·n₀|       (A ist ein Punkt auf ε, n₀ der Einheitsvektor zum Normalvektor n)

Winkel

• Zwei Geraden: φ ist der Winkel zwischen den Richtungsvektoren.

• Zwei Ebenen: φ ist der Winkel zwischen den Normalvektoren.

• Gerade und Ebene: Man berechnet zuerst den Winkel φ' zwischen dem Richtungsvektor der Gerade und dem Normalvektor der Ebene. Dann ist φ = 90° − φ'.

Flächen und Rauminhalte:

• Flächeninhalt des Parallelogramms, das von den Vektoren a und b aufgespannt wird: A = |a×b|

  Flächeninhalt des Dreiecks, das von den Vektoren a und b aufgespannt wird: A = ½·|a×b|
  Für Dreiecke im ℝ² erhält man daraus die Formel A = ½·|a_xb_y − a_yb_x|.

• Volumen des Parallelepipeds, das von den Vektoren a, b und c aufgespannt wird: V = |(a×b)·c|       (Spatprodukt)

  Volumen des Tetraeders, der von den Vektoren a, b und c aufgespannt wird: V = ¹/₆·|(a×b)·c|

Übungen