Juttas Matheseite - Kursunterlagen

Differentialrechnung

Differenzenquotient und Differentialquotient

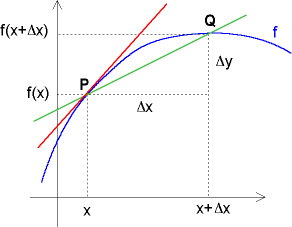
Problem: Wir suchen die Änderungsrate einer Funktion f an der Stelle x.
Geometrische Interpretation: Steigung der Tangente im Punkt P(x/f(x)).

Funktionsgraph mit Sekante PQ und Tangente P

Die Steigung der Sekante durch die Punkte P und Q (grün) beträgt

Diesen Ausdruck bezeichnet man als Differenzenquotient.

Nähert sich der Punkt Q dem Punkt P immer mehr, bis sie schließlich zusammenfallen, so geht die Sekante in die Tangente (rot) über.
Die Tangentensteigung ist also der Grenzwert der Sekantensteigung für Δx → 0 (lim = Limes = Grenzwert):

Das ist der sog. Differentialquotient oder die Ableitung der Funktion f.

Schreibweisen: (sprich: "dy nach dx"), f'(x), y'

Beispiel:

Wir suchen die Steigung der Tangente an den Graphen der Funktion f(x) = x² im Punkt P(1/1).

Steigung der Sekante:

Wenn wir Δx gegen 0 gehen lassen, erhalten wir die Steigung der Tangente:
f'(1) = 2.

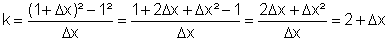
Wenn wir die Ableitung in einem beliebigen Punkt berechnen wollen, ersetzen wir in der Berechnung 1 durch x und erhalten:
f'(x) = 2·x.

In der Praxis rechnet man nicht jedesmal den Differenzenquotienten aus, sondern benutzt die folgenden

Ableitungsregeln

Ableitung der wichtigsten Funktionen:

y = c (konstant)	y' = 0
y = xⁿ	y' = n·x^n-1
y = e^x	y' = e^x
y = ln(x)
y = sin(x)	y' = cos(x)
y = cos(x)	y' = −sin(x)

Ableitungsregeln:

Konstantenregel	y = k·f(x)	y' = k·f'(x)
Summenregel	y = f(x) ± g(x)	y' = f'(x) ± g'(x)
Produktregel	y = f(x)·g(x)	y' = f'(x)·g(x) + f(x)·g'(x)
Quotientenregel
Kettenregel	y = f(g(x))	y' = f'(g(x))·g'(x) ("äußere Ableitung mal innere Ableitung")

Mit den markierten Regeln kann man bereits alle Polynomfunktionen differenzieren.

Beispiele:

y = 4·x³ + 5·x² − 3·x + 2

Konstanten- und Summenregel:

y' = 4·3x² + 5·2x − 3·1 + 0 = 12·x² + 10·x − 3
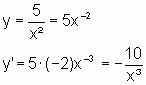
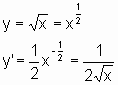
y = (x² + 1)·sin(x)

Produktregel:
f(x) = x² + 1, g(x) = sin(x)
f'(x) = 2x, g'(x) = cos(x)

y' = 2x·sin(x) + (x² + 1)·cos(x)
Quotientenregel:
f(x) = x² − 1, g(x) = x² + 2
f'(x) = 2x, g'(x) = 2x
y = (x³ + 2)⁵

Kettenregel:
f(x) = x³ + 2 = t, g(t) = t⁵
f'(x) = 3·x², g'(t) = 5·t⁴ = 5·(x³ + 2)⁴

y' = 3·x²·5·(x³ + 2)⁴ = 15·x²·(x³ + 2)⁴

Lernziele:

Ich weiß, was die Ableitung einer Funktion bedeutet.
Ich kann Polynomfunktionen differenzieren.
Ich kenne die Ableitungen der wichtigsten Funktionen.
Ich kann Potenzregel, Quotientenregel und Kettenregel anwenden.

Übungen:
Ableitung von Polynomfunktionen
Weitere Ableitungsregeln

Weiter: Kurvendiskussionen