Stammfunktionen der wichtigsten Funktionen:
| f(x) = k |
F(x) = k·x + C |
| f(x) = xn |
|
|
F(x) = ln |x| + C |
f(x) = ex |
F(x) = ex + C |
f(x) = sin(x) |
F(x) = −cos(x) + C |
f(x) = cos(x) |
F(x) = sin(x) + C |
Definition: Eine Funktion F(x) heißt Stammfunktion von f(x), wenn F'(x) = f(x).
Beispiel:
Welche Funktion hat die Ableitung f(x) = x?
Eine mögliche Antwort ist F(x) = x²/2.
Eine beliebige Stammfunktion ist von der Form F(x) = x²/2 + C (C ist eine beliebige Konstante), weil konstante Summanden beim Differenzieren wegfallen.
Wenn von der Funktion sonst nichts bekannt ist, müssen wir also immer die Integrationskonstante C dazuschreiben.
Die Stammfunktion bezeichnet man auch als unbestimmtes Integral:
F(x) = ∫f(x)·dx
("Integral von f(x) mal dx"; zur Erklärung dieser Schreibweise siehe bestimmtes Integral.)
aus der Tabelle zur Ableitung erhalten wir also leicht die Tabelle der Stammfunktionen:
Stammfunktionen der wichtigsten Funktionen:
| f(x) = k |
F(x) = k·x + C |
| f(x) = xn |
|
|
F(x) = ln |x| + C |
f(x) = ex |
F(x) = ex + C |
f(x) = sin(x) |
F(x) = −cos(x) + C |
f(x) = cos(x) |
F(x) = sin(x) + C |
:
Integrationsregeln:
∫k·f(x)·dx = k·∫f(x)·dx |
∫(f(x) ± g(x))·dx = ∫f(x)·dx ± ∫g(x)·dx |
Beispiel:
Ermittle die Gleichung der Funktion, die die Ableitung f'(x) = 2·x hat und deren Graph durch den Punkt P = (2/7) geht.
∫2·x·dx = x² + C
Koordinaten von P einsetzen:
2² + C = 7 ⇒ C = 3
f(x) = x² + 3
Wie wir wissen, erhält man die Geschwindigkeit als Ableitung der Wegfunktion und die Beschleunigung als Ableitung der Geschwindigkeitsfunktion. Umgekehrt bedeutet das: die Stammfunktion der Geschwindigkeit ergibt den Weg, die Stammfunktion der Beschleunigung die Geschwindigkeit.
| Weg: | s(t) = ∫v(t)·dt |
| Geschwindigkeit: | v(t) = ∫a(t)·dt |
Beispiel:
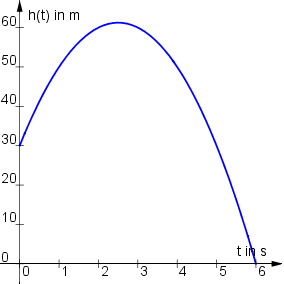
Eine Kugel wird von einem 30 m hohen Turm mit der Anfangsgeschwindigkeit 25 m/s nach oben geworfen.
Die Beschleunigung durch die Schwerkraft beträgt ca. 10 m/s².
Ermittle die Geschwindigkeit und die Höhe in Abhängigkeit von der Zeit.
(t: Zeit in Sekunden, v(t): Geschwindigkeit in m/s, h(t): Höhe in m; der Luftwiderstand wird vernachlässigt.)
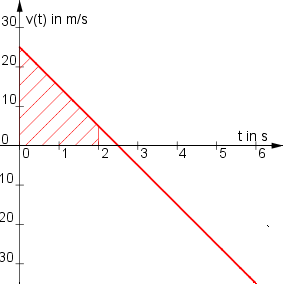
Geschwindigkeit:
a(t) = −10 (weil die Schwerkraft nach unten wirkt)
v(t) = ∫(−10)·dt = −10·t + C1
v(0) = 25 ⇒ C1 = 25
v(t) = −10·t + 25
Höhe:
h(t) = ∫(−10·t + 25)·dt = −5·t2 + 25·t + C2
h(0) = 30 ⇒ C2 = 30
h(t) = −5·t2 + 25·t + 30
Graphen der Weg- und Geschwindigkeitsfunktion:
Anmerkung:
Die Kugel legt zum Beispiel in den ersten beiden Sekunden 30 m zurück. Andrerseits beträgt die Fläche unter dem Graphen
der Geschwindigkeitsfunktion im Intervall [0; 2] (schraffiert) (25 + 5)·2/2 = 30 Flächeneinheiten. Das gilt auch für jeden anderen Zeitpunkt,
wenn man Flächenstücke unter der t-Achse negativ rechnet.
Diesen Zusammenhang zwischen Stammfunktion und Fläche werden wir im nächsten Abschnitt näher betrachten.
Lernziele
Weiter: Das bestimmte Integral