Integralrechnung

Das bestimmte Integral

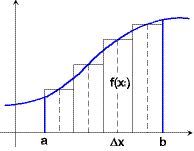
Die Funktion f(x) sei gegeben; wir wollen die Fläche zwischen dem Funktionsgraphen und der x-Achse im Intervall [a; b] berechnen.

Einen Näherungswert erhält man, wenn man [a, b] in Teilintervalle der Länge Δx teilt, in jedem Intervall eine Stelle x_i wählt und die Flächeninhalte der Rechtecke f(x_i)·Δx addiert:

A ≈ (f(x₁) + f(x₂) + ... + f(x_n))·Δx,

in Summenschreibweise:

Die Fläche - das bestimmte Integral - definieren wir als Grenzwert dieser Summe, wenn Δx gegen 0 geht; man schreibt:

sprich "Integral von a bis b von f(x) mal dx" (das Integralzeichen soll an S für "Summe" erinnern).

Man kann zeigen: Die Fläche unter dem Graphen der Funktion f (abhängig von der oberen Grenze) ist eine Stammfunktion von f.

Die Integrationskonstante muss hier nicht angegeben werden, weil sie beim Subtrahieren ohnehin wegfällt.

Für Geschwindigkeitsaufgaben bedeutet das:

Beispiele:

• 

  Wir suchen die Fläche unter dem Graphen der Funktion f(x) = x² zwischen den Grenzen a = 1 und b = 2.

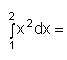  	Stammfunktion finden
  	Grenzen einsetzen, untere Grenze von oberer abziehen

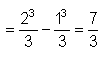• Die Geschwindigkeit eines nach oben geworfenen Körpers ist durch die Funktion v(t) = −10·t + 25 gegeben. Welchen Weg legt der Gegenstand in den ersten beiden Sekunden zurück?

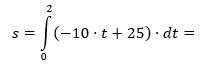  	Stammfunktion
  	Grenzen einsetzen

  Es wurden 30 Meter zurückgelegt.
  (Graphische Darstellung siehe vorige Seite)

Flächenberechnungen

Achtung: Für f(x) < 0 ist auch das Integral negativ. Der Inhalt der Fläche zwischen Kurve und x-Achse ist dann der Betrag des Integrals.

Wenn die Funktion im angegebenen Intervall ein oder mehrere Nullstellen hat, müssen wir daher die einzelnen Flächenstücke getrennt berechnen und ihre Beträge addieren.

Wenn die Fläche zwischen einer Kurve und der x-Achse berechnet werden soll (ohne dass ein Intervall angegeben ist), müssen wir zuerst die Nullstellen bestimmen - das sind dann die Integrationsgrenzen.

Die Fläche, die von den Graphen der Funktionen f(x) und g(x) eingeschlossenen wird, berechnen wir nach der Formel

Wenn es mehr als zwei Schnittpunkte gibt, muss man wieder die einzelnen Flächenstücke getrennt berechnen.

Beispiele:

• Wie groß ist die Fläche, die vom Graphen der Funktion f(x) = x² − 1 und der x-Achse zwischen den Grenzen a = 0 und b = 2 eingeschlossen wird?

  Die Funktion hat bei x₁ = 1 eine Nullstelle, wir müssen daher von 0 bis 1 und von 1 bis 2 getrennt integrieren:

  

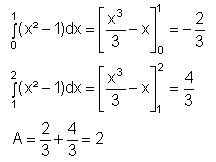
• Wie groß ist der Inhalt der Fläche, die vom Graphen der Funktion f(x) = −x³ + 3x² und der x-Achse begrenzt wird?

  Nullstellen bestimmen: −x³ + 3x² = 0 ⇒ x₁ = 0, x₂ = 3

  

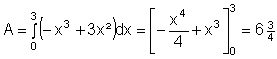
• Wie groß ist die Fläche zwischen den Graphen der Funktionen f(x) = x² und g(x) = x³?

  Schnittpunkte bestimmen: x² = x³ ⇒ x₁ = 0, x₂ = 1

  

Volumsberechnungen

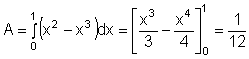
Mit Hilfe der Integralrechnung kann man auch Volumina berechnen. Wir betrachten hier nur Drehkörper (Rotationskörper).

Wenn eine Kurve um die x- oder y-Achse rotiert, kann man den entstehenden Drehkörper in schmale Schichten der Dicke Δx bzw. Δy teilen und diese näherungsweise durch Zylinder ersetzen. Ähnlich wie vorhin erhält man für das Volumen die Formeln

Rotation um die x-Achse:
Rotation um die y-Achse:

Beispiel:

• Der Graph der Funktion y = x²/4 im Intervall [0; 2] rotiert um die Koordinatenachsen. Wie groß sind die Volumina der dabei entstehenden Drehkörper?

  • Rotation um x-Achse: y² = x⁴/16, x₁ = 0, x₂ = 2
    

  • Rotation um y-Achse: x² = 4y, y₁ = 0, y₂ = 1
    

Mittelwerte von Funktionen

Um den Mittelwert (genauer: das arithmetische Mittel) mehrerer Zahlen zu berechnen, addiert man sie bekanntlich und dividiert die Summe durch die Anzahl der Werte. Wenn sich der Wert stetig ändert - wie zum Beispiel die Temperatur -, wird aus der Summe ein Integral, und man teilt durch die Länge des Integrationsintervalls.

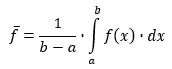
Anschauliche Interpretation: Man ersetzt die Fläche unter dier Kurve durch ein gleich großes Rechteck.

Beispiel:

• Berechne den Mittelwert der Sinusfunktion im Intervall [0; π].

  

  
  also ist

Übungen

Weitere Integrationsregeln