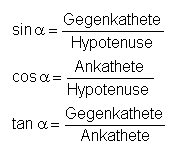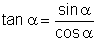Trigonometrie
"Trigonometrie" heißt wörtlich "Dreiecksvermessung"; es geht um die Beziehungen zwischen Seiten
und Winkeln in einem Dreieck.
Wiederholung einiger wichtiger Sätze:
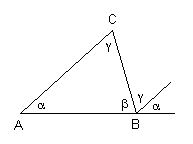 |
In jedem Dreieck beträgt die Winkelsumme α + β + γ = 180°
Der größeren Seite liegt der größere Winkel gegenüber. |
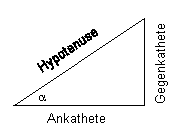 |
Im rechtwinkeligen Dreieck heißt die Seite, die dem rechten Winkel gegenüberliegt,
Hypotenuse, die anderen Seiten Katheten.
Satz von Pythagoras:
Das Quadrat der Hypotenuse ist gleich der Summe der Quadrate der Katheten. |
Winkelfunktionen im rechtwinkeligen Dreieck
Die Kathete, die dem Winkel α gegenüberliegt, bezeichnet man als
Gegenkathete von α; die Kathete, die α anliegt, ist die Ankathete von α (s. Bild oben):
Wir stellen fest: In einem rechtwinkeligen Dreieck hängt das Verhältnis zweier Seiten nur von
α ab, nicht von der Größe des Dreiecks. Man definiert daher die
Winkelfunktionen Sinus (sin), Cosinus (cos) und Tangens (tan):
Die Werte dieser Funktionen kann man in Tabellen nachschlagen oder mit dem Taschenrechner berechnen.
Ist z.B. der Wert des Sinus bekannt, und der dazugehörige Winkel wird gesucht, braucht man
die entsprechenden Umkehrfunktionen: Arcussinus (arcsin, sin−1), Arcuscosinus (arccos, cos−1)
und Arcustangens (arctan, tan−1).
Damit können wir aus zwei Bestimmungsstücken (Seiten bzw. Winkeln) eines rechtwinkeligen Dreiecks die
anderen Größen berechnen.
Als Hilfestellung kann man sich fragen: "Was ist gegeben? Was ist gesucht? Bei welcher Winkelfunktion kommen diese beiden Seiten vor?"
Beispiele:
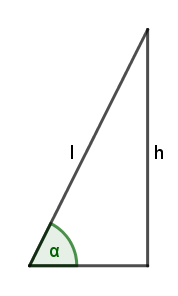
Ein Papierdrache fliegt an einer 80 m langen Schnur, die mit dem Boden den Winkel
α = 67° einschließt. Wie hoch fliegt der Drache?
Anhand einer Skizze stellen wir fest: h = Höhe = Gegenkathete von α; l = Schnurlänge = Hypotenuse.
Wir verwenden daher den Sinus:
sin(α) = h/l
h = l·sin(α) = 73,6 m
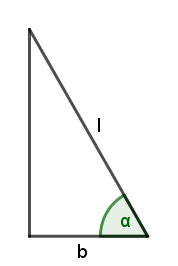
Eine Leiter lehnt an einer Wand. Sie schließt mit dem Boden den Winkel α
= 60° ein; der Fußpunkt der Leiter ist 1,2 m von der Wand entfernt. Wie lang ist die Leiter?
b = Abstand = Ankathete von α; l = Länge der Leiter = Hypotenuse.
Wir verwenden den Cosinus:
cos(α) = b/l
l = b/cos(α) = 2,4 m
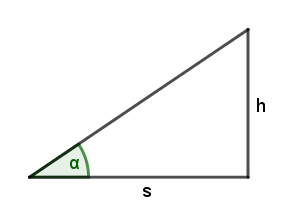
Wie hoch steht die Sonne, wenn ein 5 m langer Fahnenmast einen 7,5 m langen Schatten wirft?
α = Winkel zwischen Sonnenstrahlen und Boden; h = Höhe = Gegenkathete
von α; s = Schattenlänge = Ankathete von α.
Wir verwenden den Tangens:
tan(α) = h/s
α = tan−1(h/s) = 33,7°
Andere Figuren (Rechteck, gleichschenkeliges Dreieck, Raute ...) zerlegt man, wenn möglich,
in rechtwinkelige Dreiecke.
Es gelten folgende Beziehungen zwischen den Winkelfunktionen:
sin2 α + cos2 α = 1
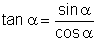
Vermessungsaufgaben
Die Trigonometrie spielt eine wichtige Rolle in der Landvermessung, weil Winkel leichter gemessen werden können als Strecken.
Winkel in einer horizontalen Ebene bezeichnet man als Horizontalwinkel, in einer vertikalen Ebene als Vertikalwinkel
(Höhen- oder Tiefenwinkel). Höhenwinkel werden immer von der Horizontalen aus nach oben gemessen, Tiefenwinkel von der Horizontalen nach unten.
Ein Sehwinkel ist der Winkel zwischen zwei beliebigen Sehrichtungen.
Beispiel:
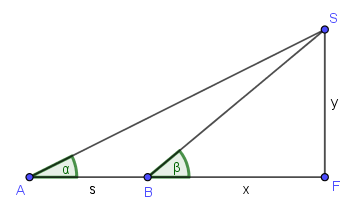
Um die Höhe eines Turms zu bestimmen, steckt man in der Ebene eine horizontale Standlinie AB = s ab, so dass A, B und der Fußpunkt F des Turms in einer Linie liegen.
Von A aus misst man zur Turmspitze S den Höhenwinkel α, von B aus den Höhenwinkel β.
Erstelle eine Formel für die Turmhöhe.
Wir bilden ein Gleichungssystem:
tan(α) = y/(x + s) ⇒ y = (x + s)·tan(α)
tan(β) = y/x ⇒ y = x·tan(β)
(x + s)·tan(α) = x·tan(β) (gleichsetzen)
x = s·tan(α)/(tan(β) − tan(α))
y = x·tan(β) = s·tan(α)·tan(β)/(tan(β) − tan(α))
Ausführliche Erklärung:
mathe online, Winkelfunktionen: http://www.mathe-online.at/mathint/wfun/i.html
Lernziele
- Ich kenne die Definitionen von Sinus, Cosinus und Tangens im rechtwinkeligen Dreieck.
- Ich kann rechtwinkelige Dreiecke mit Hilfe von Winkelfunktionen auflösen.
- (Ich kenne die wichtigsten Beziehungen zwischen den Winkelfunktionen.)
Übungen
Historische chinesische Vermessungsaufgabe