Ungleichungen mit zwei Unbekannten

Die Lösungsmenge der Gleichung a·x + b·y = c lässt sich als Gerade darstellen (siehe Gleichungen). Diese Gerade teilt die Ebene in zwei Halbebenen. Für alle Punkte auf der einen Seite der Geraden gilt a·x + b·y < c, auf der anderen Seite a·x + b·y > c.

Die Lösungsmenge der Ungleichung

a·x + b·y < c       bzw.       a·x + b·y > c

entspricht daher einer offenen Halbebene (ohne Randgerade),
die Lösungsmenge der Ungleichung

a·x + b·y ≤ c       bzw.       a·x + b·y ≥ c

einer abgeschlossenen Halbebene (einschließlich Randgerade).
Auf welcher Seite welches Vorzeichen gilt, kann man leicht durch Einsetzen eines Punktes, z.B. (0/0), feststellen.

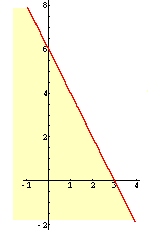
Beispiel: Die Abbildung zeigt die Lösungsmenge der Umgleichung 2·x + y ≤ 6.

Die Lösungsmenge eines Ungleichungssystems ist der Durchschnitt der entsprechenden Halbebenen. Das ist im Allgemeinen ein konvexes Vieleck (d.h. ohne einspringende Ecken), sie kann aber auch leer sein.

Lineare Optimierung

In der Praxis stellt sich oft das Problem, eine bestimmte Größe, die sogenannte Zielfunktion, zu optimieren (z.B. soll der Gewinn maximal oder die Kosten minimal werden). Diese Funktion hängt von mehreren Variablen ab, die aber bestimmte einschränkende Nebenbedingungen einhalten müssen (z.B. begrenzte Material- oder Zeitressourcen). Wenn sich Zielfunktion und Nebenbedingungen durch lineare Gleichungen bzw. Ungleichungen ausdrücken lassen, spricht man von linearer Optimierung. Optimierungsprobleme mit zwei Variablen können graphisch gelöst werden.

Beispiel:
Ein Weinhändler verkauft Weißwein und Rotwein. Er kann pro Tag von jeder Sorte höchstens 20 Flaschen verkaufen, insgesamt höchstens 30 Flaschen. Bei einer Flasche Weißwein beträgt sein Gewinn 1 €, bei einer Flasche Rotwein 2 €. Wie viele Flaschen muss er von jeder Sorte verkaufen, damit sein Gewinn maximal wird?

Wir bezeichnen die Menge an Weißwein mit x, die Menge an Rotwein mit y. Die Zielfunktion (der Gewinn) lautet

z(x,y) = x + 2·y → Maximum

Die Nebenbedingungen schreiben wir als Ungleichungen:

I:	x	≤ 20
II:	y	≤ 20
III:	x + y	≤ 30
IV:	x	≥ 0
V:	y	≥ 0

Die letzten beiden Ungleichungen sind die sogenannten Nichtnegativitätsbedingungen - der Händler kann ja keine negativen Mengen verkaufen.

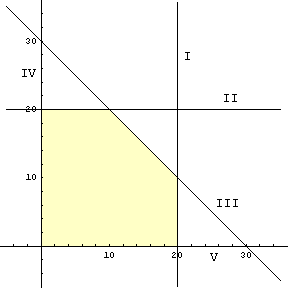
Wir zeichnen die Lösungsmenge dieses Ungleichungssystems, den sogenannten zulässigen Bereich:

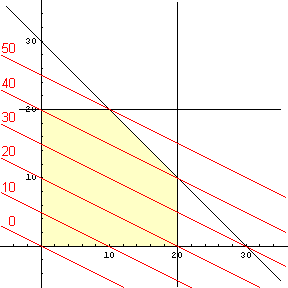Die Linien, auf denen die Zielfunktion einen konstanten Wert annimmt (sozusagen die Höhenlinien), sind parallele Geraden. Es genügt daher, eine solche Gerade zu zeichnen (z.B. für z = 0) und so weit wie möglich nach oben zu verschieben, so dass sie den zulässigen Bereich gerade noch berührt. Wie wir sehen, ist das im Schnittpunkt der Geraden II und III der Fall, also für x = 10, y = 20. In diesem Punkt nimmt die Zielfunktion den größtmöglichen Wert an.

(Eine andere Möglichkeit wäre, die Koordinaten aller Eckpunkte auszurechnen und in die Zielfunktion einzusetzen.)

Der Händler soll also 10 Flaschen Weißwein und 20 Flaschen Rotwein verkaufen. Sein Gewinn beträgt dann z(10,20) = 10 + 2·20 = 50 €.

Wenn das Minimum der Zielfunktion gesucht ist, muss man die Höhenlinie so weit wie möglich nach unten verschieben.

Die Zielfunktion nimmt ihren optimalen Wert immer am Rand des zulässigen Bereichs an - entweder in einem Eckpunkt oder, wenn die Höhenlinien zu einer Randgeraden parallel sind, auf einer Strecke. In diesem Fall stellen alle Punkte der Strecke gleichwertige Lösungen dar.

Auf http://statistik.wu-wien.ac.at/~leydold/MOK/HTML/node146.html gibt es eine Erklärung auf etwas wissenschaftlicherem Niveau.

Übungen